Bean Type Classification Using Decision Trees

Machine Learning
Decision Trees
Tuning
Author

Olamide Adu

Published

December 12, 2024

Introduction

The aim of this blog post is to use decision tree machine learning algorithm to classify dry bean based on some features. This is a Kaggle challenge dataset. Images of 13,611 grains of 7 different registered dry beans were taken with a high-resolution camera. A total of 16 features; 12 dimensions and 4 shape forms, were obtained from the grains. The features of the data are:

Dry Beans Featured.
Feature Description
Area (A) The area of a bean zone and the number of pixels within its boundaries.
Perimeter (P) Bean circumference is defined as the length of its border.
Major axis length (L) The distance between the ends of the longest line that can be drawn from a bean.
Minor axis length (l) The longest line that can be drawn from the bean while standing perpendicular to the main axis.
Aspect ratio (K) Defines the relationship between L and l.
Eccentricity (Ec) Eccentricity of the ellipse having the same moments as the region.
Convex area (C) Number of pixels in the smallest convex polygon that can contain the area of a bean seed.
Equivalent diameter (Ed) The diameter of a circle having the same area as a bean seed area.
Extent (Ex) The ratio of the pixels in the bounding box to the bean area.
Solidity (S) Also known as convexity. The ratio of the pixels in the convex shell to those found in beans.
Roundness (R) Calculated with the following formula: (4piA)/(P^2)
Compactness (CO) Measures the roundness of an object: Ed/L
ShapeFactor1 (SF1)
ShapeFactor2 (SF2)
ShapeFactor3 (SF3)
ShapeFactor4 (SF4)
Class Seker, Barbunya, Bombay, Cali, Dermosan, Horoz and Sira

Load Packages

To begin, we load the necessary packages. I also set the extra swatch color, just in case we have more than the default provided by ggthemr. I have recently fell in love with using the ggthemr package by Mikata-Project.

pacman::p_load(
  tidymodels, tidyverse, ggthemr, farff,
  earth, rpart.plot, vip, corrplot, skimr
)

ggthemr(
  palette = "flat dark",
  layout = "clean",
  spacing = 2,
  type = "outer"
)

darken_swatch(amount = .1)
additional_colors <- c("#af4242", "#535364", "#FFC300", "#e09263", "#123367", "salmon", "#c0ca33", "#689f38", "#e53935")

set_swatch(c(unique(swatch()), additional_colors))

This is the first time I am seeing a data with a .arffextension, so, I searched online immediately to see if there’s a package to import a data with an arff extension in R. The best place to search for this is CRAN, of course Google will also give very good result, but I choose CRAN regardless. Fortunately, there’s the farrf package with development starting in 2015 by mlr-org. The package is also pretty straightforward to use. Interestingly the package imports data as data.frame, which is great. Afterwards, I converted to tibble.

bean_tbl <- readARFF("data/Dry_Bean_Dataset.arff") |> 
  janitor::clean_names() |> 
  as_tibble()

head(bean_tbl)
# A tibble: 6 × 17
   area perimeter major_axis_length minor_axis_length aspect_ration eccentricity
  <dbl>     <dbl>             <dbl>             <dbl>         <dbl>        <dbl>
1 28395      610.              208.              174.          1.20        0.550
2 28734      638.              201.              183.          1.10        0.412
3 29380      624.              213.              176.          1.21        0.563
4 30008      646.              211.              183.          1.15        0.499
5 30140      620.              202.              190.          1.06        0.334
6 30279      635.              213.              182.          1.17        0.520
# ℹ 11 more variables: convex_area <dbl>, equiv_diameter <dbl>, extent <dbl>,
#   solidity <dbl>, roundness <dbl>, compactness <dbl>, shape_factor1 <dbl>,
#   shape_factor2 <dbl>, shape_factor3 <dbl>, shape_factor4 <dbl>, class <fct>

Exploratory Datta Analysis

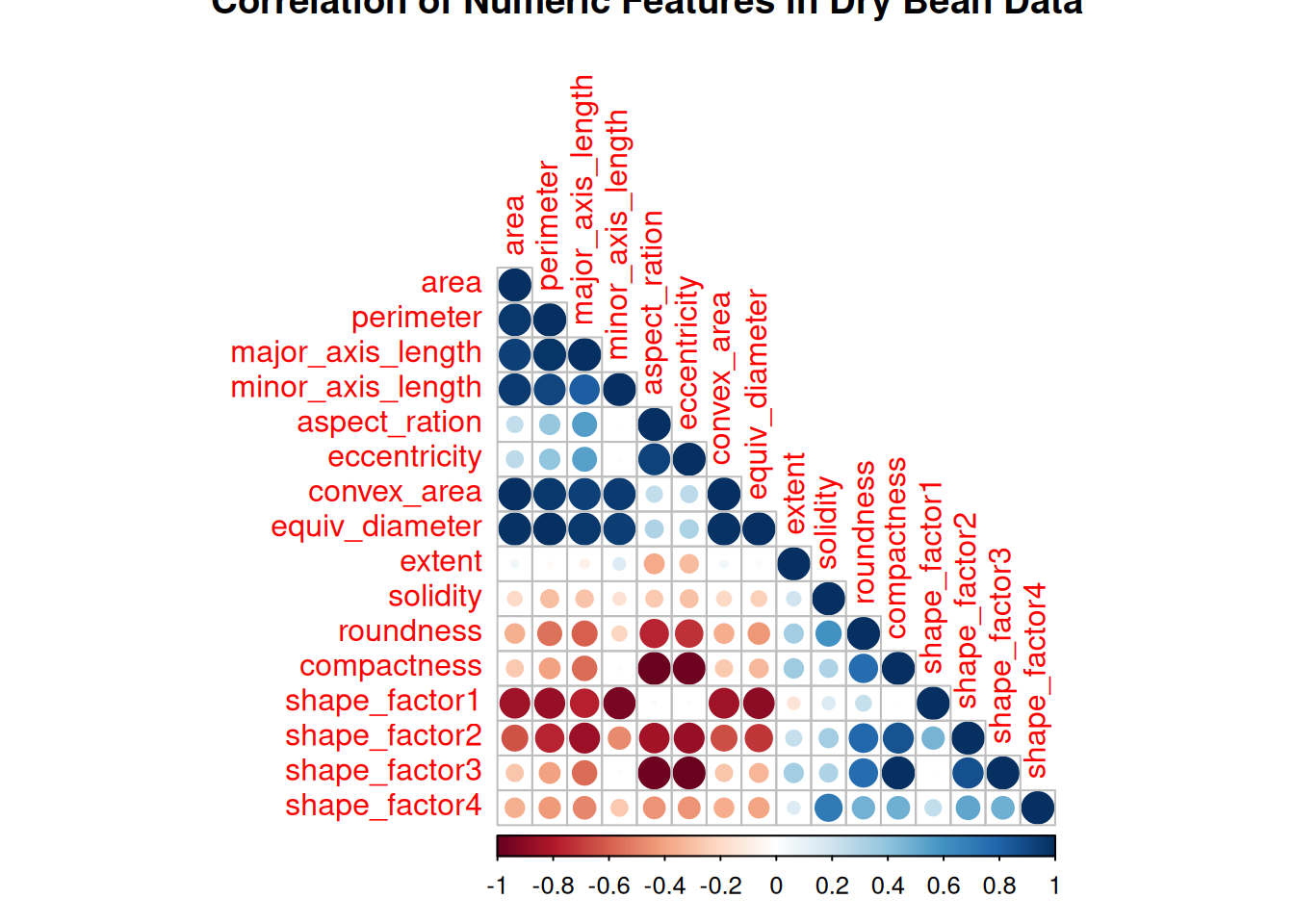
Next is EDA, this will be quick and short. Table 1 shows a good summary of the data including the data types, and information on the completeness of the data. From what the result in Table 1 (a) and Table 1 (b) the data is complete. Figure 1 shows the correlation matrix of the numeric variables.

skim(bean_tbl)
Table 1: Data summary
(a)
Name bean_tbl
Number of rows 13611
Number of columns 17
_______________________
Column type frequency:
factor 1
numeric 16
________________________
Group variables None

Variable type: factor

(b)
skim_variable n_missing complete_rate ordered n_unique top_counts
class 0 1 FALSE 7 DER: 3546, SIR: 2636, SEK: 2027, HOR: 1928

Variable type: numeric

(c)
skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
area 0 1 53048.28 29324.10 20420.00 36328.00 44652.00 61332.00 254616.00 ▇▂▁▁▁
perimeter 0 1 855.28 214.29 524.74 703.52 794.94 977.21 1985.37 ▇▆▁▁▁
major_axis_length 0 1 320.14 85.69 183.60 253.30 296.88 376.50 738.86 ▇▆▂▁▁
minor_axis_length 0 1 202.27 44.97 122.51 175.85 192.43 217.03 460.20 ▇▇▁▁▁
aspect_ration 0 1 1.58 0.25 1.02 1.43 1.55 1.71 2.43 ▂▇▅▂▁
eccentricity 0 1 0.75 0.09 0.22 0.72 0.76 0.81 0.91 ▁▁▂▇▇
convex_area 0 1 53768.20 29774.92 20684.00 36714.50 45178.00 62294.00 263261.00 ▇▂▁▁▁
equiv_diameter 0 1 253.06 59.18 161.24 215.07 238.44 279.45 569.37 ▇▆▁▁▁
extent 0 1 0.75 0.05 0.56 0.72 0.76 0.79 0.87 ▁▁▅▇▂
solidity 0 1 0.99 0.00 0.92 0.99 0.99 0.99 0.99 ▁▁▁▁▇
roundness 0 1 0.87 0.06 0.49 0.83 0.88 0.92 0.99 ▁▁▂▇▇
compactness 0 1 0.80 0.06 0.64 0.76 0.80 0.83 0.99 ▂▅▇▂▁
shape_factor1 0 1 0.01 0.00 0.00 0.01 0.01 0.01 0.01 ▁▃▇▃▁
shape_factor2 0 1 0.00 0.00 0.00 0.00 0.00 0.00 0.00 ▇▇▇▃▁
shape_factor3 0 1 0.64 0.10 0.41 0.58 0.64 0.70 0.97 ▂▇▇▃▁
shape_factor4 0 1 1.00 0.00 0.95 0.99 1.00 1.00 1.00 ▁▁▁▁▇ 
corrplot(
  cor(bean_tbl[, 1:16]),
  method = "circle",
  addrect = 2,
  pch = 5,
  title = "Correlation of Numeric Features in Dry Bean Data",
  type = "lower"
)
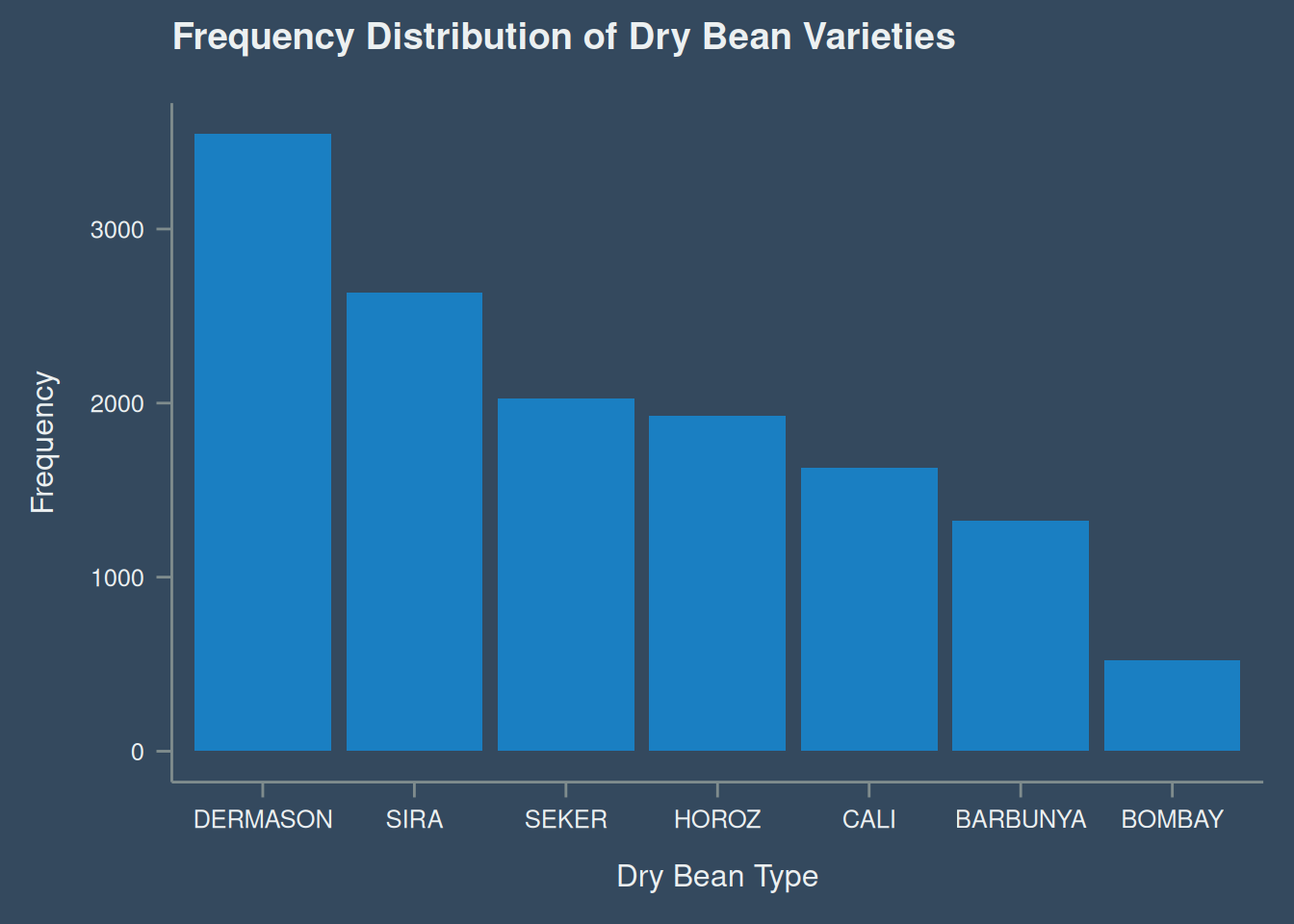
Figure 1: Correlation of bean features

The frequency of the different types of dry bean is shown in Figure 2.

bean_tbl |> 
  ggplot(aes(fct_infreq(class))) +
  geom_bar() +
  labs(
    x = "Dry Bean Type",
    y = "Frequency",
    title = "Frequency Distribution of Dry Bean Varieties"
  )
Figure 2: Frequency distribution of dry-bean varieties. Dermason occurs the most and Bombay is the least occuring bean type.

Modeling

Data Shairing

The data was split to two, a testing data, which is 30% the number of records of the original data and 70% for the training data. To ensure reproducibility, a seed was set.

set.seed(122)
bean_split <- initial_split(bean_tbl, prop = .7, strata = class)
bean_split
<Training/Testing/Total>
<9525/4086/13611>
bean_train <- training(bean_split)

Resamples of the training data was also set at 10 folds, which I think has continuously been the go-to value for number of folds.

bean_folds <- vfold_cv(bean_train, v = 10)

Model Specification

As stated earlier, decision tree model will be used in this post.

dt_spec <- decision_tree(
  cost_complexity = tune(),
  tree_depth = tune(),
  min_n = tune()
) |> 
  set_mode("classification") |> 
  set_engine("rpart")

dt_spec
Decision Tree Model Specification (classification)

Main Arguments:
  cost_complexity = tune()
  tree_depth = tune()
  min_n = tune()

Computational engine: rpart

Decision trees does not require a lot of preprocessing. So, the stating the family will be the only preprocessing step.

dt_rec <- recipe(class ~ ., data = bean_train)

dt_wf <- workflow() |> 
  add_recipe(dt_rec) |> 
  add_model(dt_spec)

dt_wf
══ Workflow ════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: decision_tree()

── Preprocessor ────────────────────────────────────────────────────────────────
0 Recipe Steps

── Model ───────────────────────────────────────────────────────────────────────
Decision Tree Model Specification (classification)

Main Arguments:
  cost_complexity = tune()
  tree_depth = tune()
  min_n = tune()

Computational engine: rpart

Model Tuning

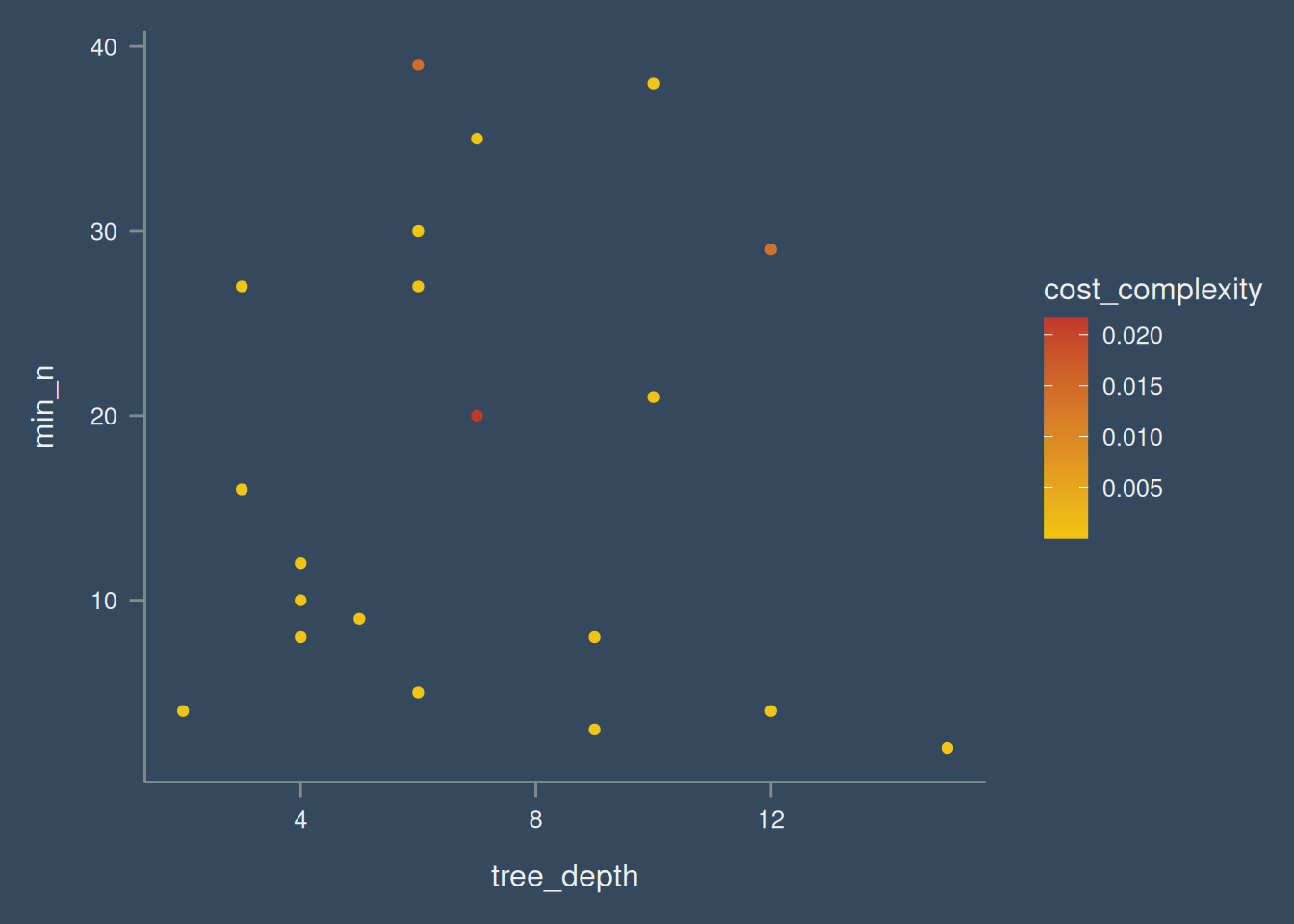
After model specification, a grid can be randomly generated from the tune parameters. see Figure 3 for the tune grid.

set.seed(122)

dt_grid <- dt_spec |> 
  extract_parameter_set_dials() |> 
  grid_random(size = 20)


dt_grid |> 
  ggplot(aes(tree_depth, min_n, col = cost_complexity)) +
  geom_point() +
  scale_color_continuous()
Figure 3: Decision tune parameter grid

After the ground works are down. The parameter needs to be tuned.

dt_tune <- tune_grid(
  object = dt_wf,
  resamples = bean_folds,
  grid = dt_grid,
  control = control_grid(save_pred = TRUE, save_workflow = TRUE)
)

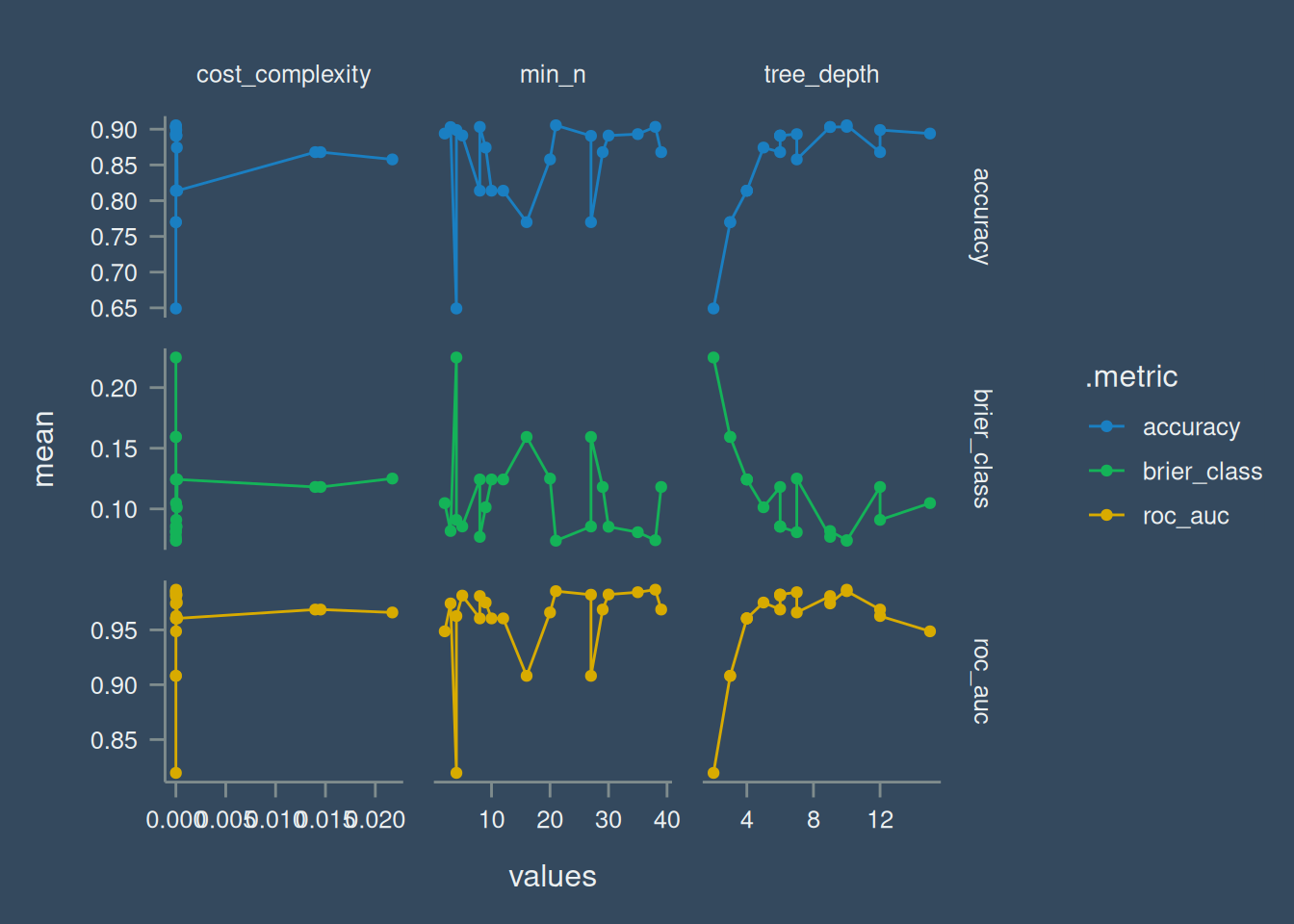
Results from tuning is shown in Table 2 with, represented visually in Figure 4 three metrics to measure which combination of the parameters would give the best result.

Table 2: Tuning result from tuning parameters with three metric from two estimators to measure the best model from the combination of the three parameters 
dt_tune |> 
  collect_metrics()
# A tibble: 60 × 9
   cost_complexity tree_depth min_n .metric     .estimator   mean     n  std_err
             <dbl>      <int> <int> <chr>       <chr>       <dbl> <int>    <dbl>
 1        1.06e-10          7    35 accuracy    multiclass 0.893     10 0.00270 
 2        1.06e-10          7    35 brier_class multiclass 0.0808    10 0.00215 
 3        1.06e-10          7    35 roc_auc     hand_till  0.984     10 0.000989
 4        1.79e-10          9     8 accuracy    multiclass 0.903     10 0.00298 
 5        1.79e-10          9     8 brier_class multiclass 0.0769    10 0.00260 
 6        1.79e-10          9     8 roc_auc     hand_till  0.981     10 0.00147 
 7        2.10e-10          2     4 accuracy    multiclass 0.649     10 0.00230 
 8        2.10e-10          2     4 brier_class multiclass 0.225     10 0.00103 
 9        2.10e-10          2     4 roc_auc     hand_till  0.820     10 0.00112 
10        2.33e-10          6    27 accuracy    multiclass 0.891     10 0.00253 
# ℹ 50 more rows
# ℹ 1 more variable: .config <chr>

Visually, this is represented below:

dt_tune |> 
  collect_metrics() |> 
  pivot_longer(
    cols = cost_complexity:min_n,
    names_to = "params",
    values_to = "values"
  ) |> 
  ggplot(aes(values, mean, colour = .metric)) +
  geom_point() +
  geom_line() +
  facet_grid(.metric~params, scales = "free")
Warning: The `scale_name` argument of `discrete_scale()` is deprecated as of ggplot2
3.5.0.
Figure 4

Final FIt

Next we extract the best combination of the parameters using roc_auc as the evaluation metric.

best_tune <- dt_tune |> 
  select_best(metric = "roc_auc")

best_tune
# A tibble: 1 × 4
  cost_complexity tree_depth min_n .config         
            <dbl>      <int> <int> <chr>           
1       0.0000163         10    38 pre0_mod10_post0

Next, we refit the best tune parameter to the workflow.

dt_wf <- dt_tune |>
  extract_workflow()

dt_fwf <- finalize_workflow(
  dt_wf,
  best_tune
)

dt_fwf
══ Workflow ════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: decision_tree()

── Preprocessor ────────────────────────────────────────────────────────────────
0 Recipe Steps

── Model ───────────────────────────────────────────────────────────────────────
Decision Tree Model Specification (classification)

Main Arguments:
  cost_complexity = 1.62802544691579e-05
  tree_depth = 10
  min_n = 38

Computational engine: rpart 
dt_final_fit <- dt_fwf |> 
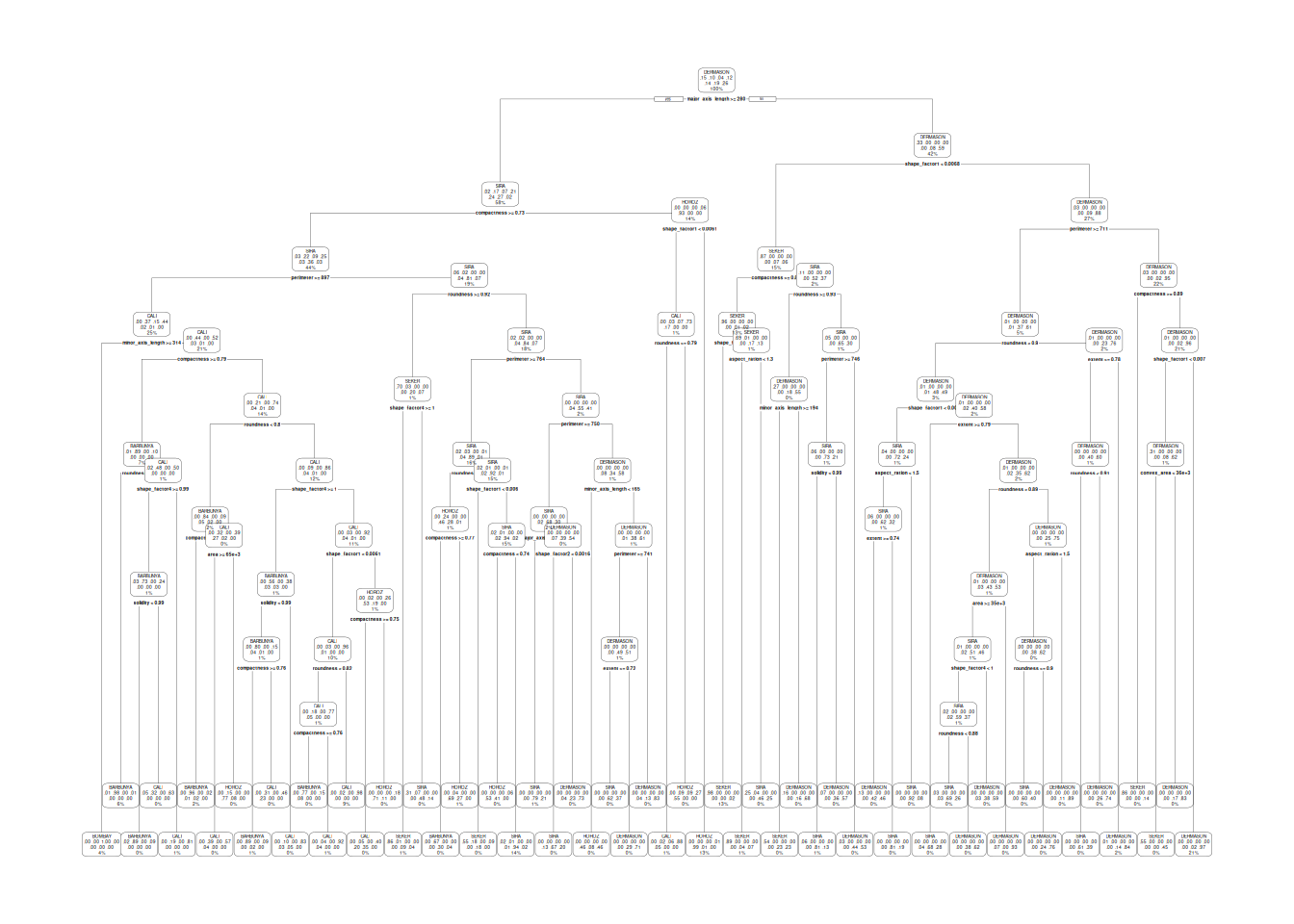
  last_fit(bean_split)

A visualization of how the features are used in determining the class of the dry-beans is shown in Figure 5.

dt_final_fit |> 
  extract_fit_engine() |> 
  rpart.plot::rpart.plot()
Figure 5: Dendrogram showing how decision trees predict their variables.

Variable Importance Plot

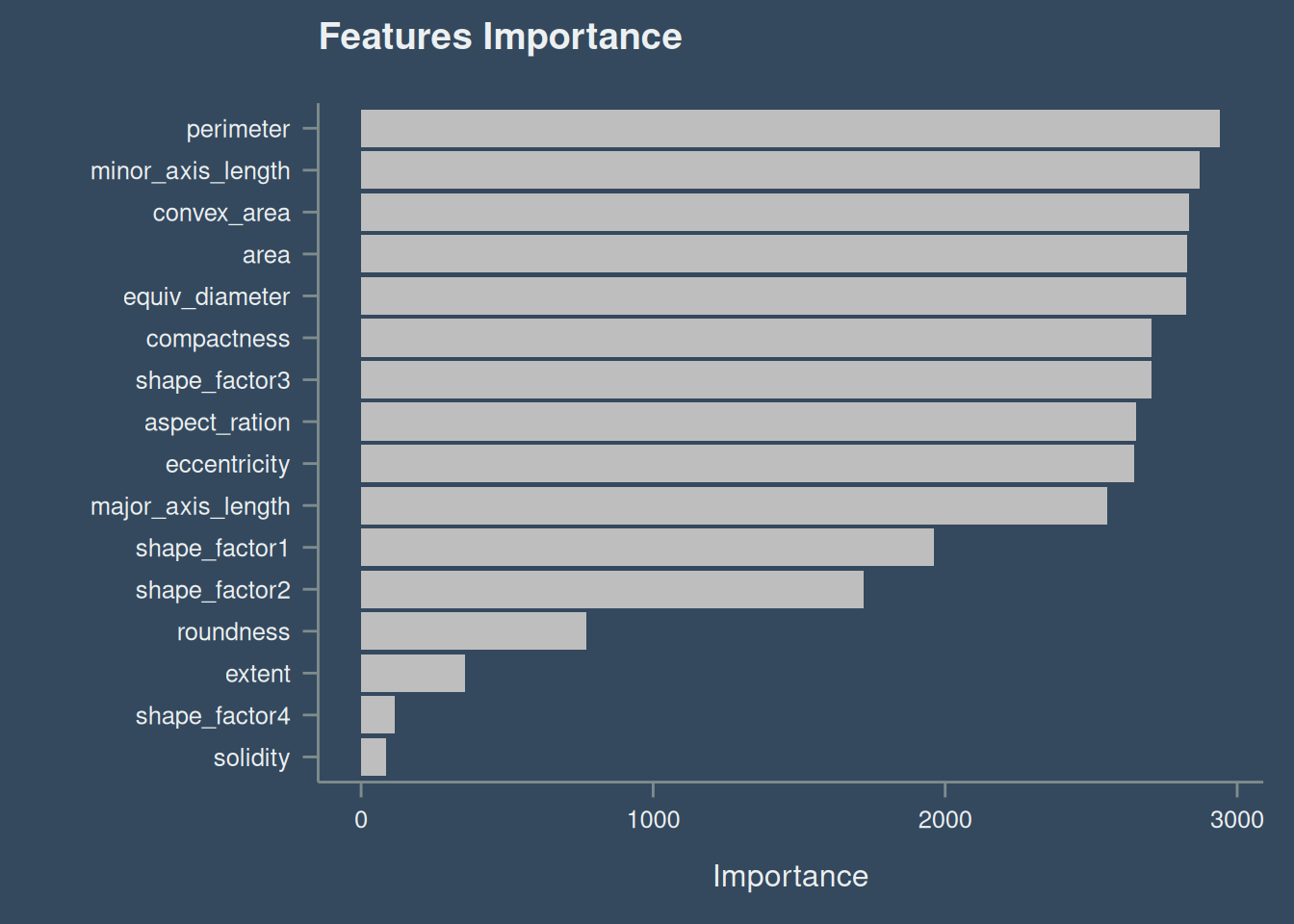
The feature perimeter have the largest effect on the model, while solidity have the least effect. Check Figure 6

dt_final_fit |> 
  extract_fit_engine() |> 
  vip(
    geom = "col",
    num_features = 17,
    aesthetics = list(
      fill = "gray",
      size = 1.5
    )
  ) +
  ggtitle("Features Importance")
Figure 6: Variable importance plots shows solidity, shape_factor4, extent, and roundness contribute less to the model, while perimeter, area related features and minor_axis_length contibuted the most to the model.